Fonctionnement d'un réacteur nucléaire
Une centrale nucléaire est une usine qui produit de l' électricité à partir de la désintégration de l' uranium. L' uranium, en se désintégrant, libère de la chaleur, la chaleur fait évaporer de l' eau sous forme de vapeur, la vapeur fait tourner une turbine, et la turbine entraîne un alternateur qui produit de l' électricité. (cf Site du SFEN)
D'où vient l' énergie de l' uranium ?
L' Uranium est composé de plusieurs isotopes, principalement l' uranium 235, 238, et quelques traces de 232. L' Uranium est un noyau lourd, car composé de 92 protons.
Or tous les atomes comportant plus de 86 protons sont radioactifs. Cf graphe:
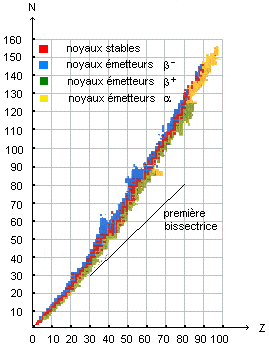
Isotopes radioactifs
L' uranium 235 a l' avantage qu' il peut se désintégrer si on le bombarde d' un neutron.
La première équation de désintégration est la plus courante. On se fondera sur cette équation dans la suite du TPE. On le voir sur les équations, en se désintégrant, l' atome d' uranium libère 1, 2 ou 3 neutrons, c' est à dire autant ou plus de neutrons qu' il en a " absorbé ". Ces neutrons peuvent à leur tour désintégrer des autres atomes d' uranium, qui à leur tours vont libérer encore plus de neutrons… C' est la réaction en chaîne.
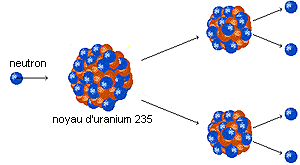
Principe de la réaction en chaîne
Calculons la variation de la masse lors de la désintégration d' un noyau d' uranium 235.
+ + 2
Masses des particules m( ) = 234,9935u;
m( ) = 93,8945u;
mn = 1,0087u
m( ) = 139,8920u
m = m( ) + m( ) + 2.mn - m( ) + mn
m = m( ) + m( ) + mn - m( )
m = 93,8945 + 139,8920 + 1,0087 - 234,9935
m = -0,1983u
Or, le savant Albert Einstein, lors de sa théorie sur la relativité, a exprimé la célèbre formule : E= m.C²
Ce qui revient dire que l' énergie d' un objet = sa masse fois la vitesse de la lumière au carré. Donc la masse, c' est de l' énergie.
Or, lors de la fission d' un atome d' U235, il y a perte de masse.
Donc il y a libération d' énergie. L' énergie libérée vaut - m (car le systeme ayant perdu de la masse, de l' énergie a été fournie au milieu extérieur), multipliée à la masse de l' unité arbitraire, 1,6749.10-27, multipliée à la vitesse de la lumière au carré, exprimée en m.s-1
E = | m|.c2 => E = 0,1983 x 1,6749.10-27 x (3.10^8)²
=> E = 2,99.10-11J
=> E = 186,8MeV
1 eV= 1,60.10-19 J
Un atome d' uranium libère 186,8 MeV en se désintégrant, soit 2,9888.10-11 Joules
Une mole d' uranium libère donc :
E= Na * 2,9888.10-11
E=6,022.1023* 2,9888.10-11
E=17,999*10^12
E= 1,8*10^13 Joules
Où Na désigne le nombre d'Avogadro, c' est à dire le nombre d' atomes de carbones 12 dans 12 grammes de Carbone. Na est la valeur admise du nombre d' atomes dans une mol d' un élément donné.
La désintégration complète d' une mole d' uranium 235 (235 grammes) libère 1,8*10^13 Joules, soit 5 GWH.
Bien que les centrales nucléaires actuelles n' ont des rendements que de 34%, elles arrivent donc à produite 1,7 Gwh par mol d' uranium, autant qu' avec 600 tonnes de charbon pour les centrales thermiques classiques.
Les centrales nucléaire, bien que dangereuses à cause de la radioactifs des produits de la fission nucléaire, et de leurs coûts élevés, ont vite intéressés de nombreux pays notamment la France, la Russie et les Etats-Unis, car elles garantissent une indépendance énergétique, et permettent de limiter l' émission de gaz polluants.
Envie d'aider le site? De me poser une question? N'hésitez pas à nous contacter
Vous avez aimé le site? N'hésitez pas à le mettre en Page de démarrage